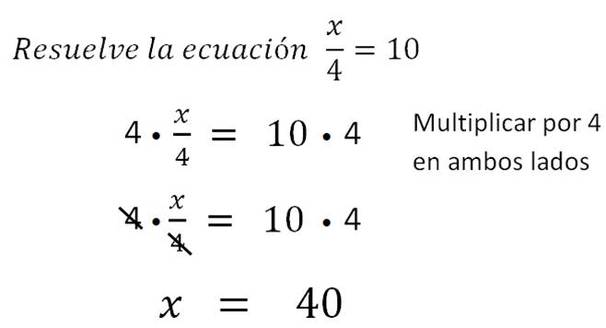Ecuación
Una ecuación lleva un signo de igualdad para indicar que dos expresiones son iguales.
Ecuaciones lineales en una variable
Es una ecuación en la que aparece una variable elevada al exponente uno.
La variable puede aparecer por más de una ocasión, por ejemplo, en la ecuación 5n – 3 = 3n + 1 es una ecuación de primer grado en una variable. Observa que la variable n aparece dos veces pero ambas elevadas al exponente uno.
Ejemplos de ecuaciones lineales son:
x + 4 = 11; 3y = 75; m - 12 = 90; n/7 = 8
La variable puede aparecer por más de una ocasión, por ejemplo, en la ecuación 5n – 3 = 3n + 1 es una ecuación de primer grado en una variable. Observa que la variable n aparece dos veces pero ambas elevadas al exponente uno.
Ejemplos de ecuaciones lineales son:
x + 4 = 11; 3y = 75; m - 12 = 90; n/7 = 8
Resolver una ecuación lineal en una variable
Tienes que hallar el valor de la variable que hace correcta la ecuación. Este valor es la solución o la raíz de la ecuación.
Por ejemplo, ¿es 2 una solución de la ecuación 5n – 3 = 3n + 1? Si lo es, pues al sustituir el valor de 2 en la ecuación observamos que es cierta la igualdad:
5(2) – 3 = 3(2) + 1
10 – 3 = 6 + 1
7 = 7 Cierto
Lo que hacemos para resolver una ecuación lineal en una variable es despejar para la variable, es decir, dejarla a un lado de la ecuación y escribir las constantes (los números) al otro lado de la ecuación usando las propiedades
correspondientes:
1. Si a = b, entonces a + c = b + c y a – c = b – c.
2. Si a = b y c ≠0, entonces:
Por ejemplo, ¿es 2 una solución de la ecuación 5n – 3 = 3n + 1? Si lo es, pues al sustituir el valor de 2 en la ecuación observamos que es cierta la igualdad:
5(2) – 3 = 3(2) + 1
10 – 3 = 6 + 1
7 = 7 Cierto
Lo que hacemos para resolver una ecuación lineal en una variable es despejar para la variable, es decir, dejarla a un lado de la ecuación y escribir las constantes (los números) al otro lado de la ecuación usando las propiedades
correspondientes:
1. Si a = b, entonces a + c = b + c y a – c = b – c.
2. Si a = b y c ≠0, entonces:
Video para resolver ecuación lineal con suma
http://www.phschool.com/atschool/academy123/spanish/academy123_content/wl-book-demo/ph-013ss.html
Video para resolver una ecuación con resta
http://www.phschool.com/atschool/academy123/spanish/academy123_content/wl-book-demo/ph-012ss.html
Video para resolver una ecuación simple con multiplicación
http://www.phschool.com/atschool/academy123/spanish/academy123_content/wl-book-demo/ph-015ss.html
Video para resolver una ecuación simple con división
http://www.phschool.com/atschool/academy123/spanish/academy123_content/wl-book-demo/ph-014ss.html
Video para resolver una ecuación con dos pasos
http://www.phschool.com/atschool/academy123/spanish/academy123_content/wl-book-demo/ph-162ss.html
Resolver ecuaciones lineales usando una balanza
http://nlvm.usu.edu/es/nav/frames_asid_201_g_4_t_2.html?open=instructions&from=category_g_4_t_2.html
Resolver ecuaciones de dos pasos
Ejemplo 1:
Resuelve x + 9 = 20
- 9 - 9 Restar 9 en ambos lados de la ecuación
x + 0 = 11
x = 11
- 9 - 9 Restar 9 en ambos lados de la ecuación
x + 0 = 11
x = 11
Ejemplo 2:
Resuelve x - 10 = 20
+ 10 + 10 Sumar 10 en ambos lados de la ecuación
x + 0 = 30
x = 30
+ 10 + 10 Sumar 10 en ambos lados de la ecuación
x + 0 = 30
x = 30
Ejemplo 3:
Resuelve 3x = 24
3x = 24 Dividir entre 3 en ambos lados de la ecuación
3 3
x = 8
3x = 24 Dividir entre 3 en ambos lados de la ecuación
3 3
x = 8
Ejemplo 4:
Ejemplo 5:
Resuelve 3x + 8 = 2
3x + 8 = 2
- 8 - 8 Restar 8 en ambos lados
3x + 0 = -6
3x = -6 Dividir entre 3 en ambos lados
3 3
x = -2
3x + 8 = 2
- 8 - 8 Restar 8 en ambos lados
3x + 0 = -6
3x = -6 Dividir entre 3 en ambos lados
3 3
x = -2
Ejemplo 6:
Determina el valor de la variable en:
5(x - 7) = 0
5 ( 0 ) = 0
entonces: x - 7 = 0
+ 7 + 7
x = 7
Haz clic en el enlace abajo para ver una lección interactiva sobre ecuación lineal en una variable
http://www.skoool.es/content/los/maths/linear_eq/launch.html
Presentación
Baja el archivo de PowerPoint y estudia los ejercicios mostrados
| resolver_ecuaciones_en_una_variable.ppt | |
| File Size: | 481 kb |
| File Type: | ppt |